In the realm of quantitative finance, the modeling of interest rate dynamics stands as a fundamental pillar of modern financial theory. The ability to accurately model and forecast interest rates is not merely a technical exercise but a critical component in the valuation of financial instruments, risk management, and strategic decision-making. This article delves into the theoretical foundations and practical applications of two seminal interest rate models: the Vasicek and Cox–Ingersoll–Ross (CIR) models, exploring their mathematical underpinnings, estimation methodologies, and implications for financial markets.

Theoretical Foundations

The evolution of interest rate modeling has been driven by the need to capture the complex dynamics of financial markets. At its core, interest rate modeling seeks to describe the stochastic behavior of rates through time, accounting for mean reversion, volatility, and the possibility of negative rates. The theoretical framework we explore here represents a significant advancement in our understanding of these dynamics.

Vasicek Model: A Mean-Reverting Process

The Vasicek model, introduced in 1977, represents a groundbreaking approach to interest rate modeling. It is based on the Ornstein–Uhlenbeck process, a continuous-time stochastic process that exhibits mean reversion:

Where:

• rt represents the instantaneous interest rate
• a denotes the speed of mean reversion
• b is the long-term mean level
• σ is the volatility parameter
• Wt is a Wiener process (Brownian motion)

This model's theoretical elegance lies in its ability to capture the tendency of interest rates to revert to a long-term mean while allowing for stochastic fluctuations. However, its assumption of constant volatility and the possibility of negative rates present theoretical limitations that the CIR model seeks to address.

CIR Model: A Square-Root Process

The Cox–Ingersoll–Ross model, developed in 1985, extends the Vasicek framework by introducing a square-root term in the volatility component:

This modification has profound theoretical implications:

• The volatility term σ√rt ensures that rates remain non-negative
• The square-root process maintains the mean-reverting property
• The model preserves analytical tractability while adding realism

Estimation and Calibration

The theoretical framework must be grounded in empirical data through careful parameter estimation. Our approach combines maximum likelihood estimation with advanced optimization techniques:

Data Sources and Preparation

To ensure robustness of our analysis, we utilize data from the U.S. Department of the Treasury (https://home.treasury.gov/), focusing specifically on the 1-year Treasury yield. This data source provides reliable, high-frequency observations of interest rate movements in the world's largest sovereign debt market, making it ideal for calibrating our models. The historical yields were preprocessed to account for weekends and holidays, with appropriate interpolation methods applied where necessary.

Vasicek Parameter Estimation

For the Vasicek model, we employ maximum likelihood estimation, which provides consistent and efficient parameter estimates under the model's assumptions. The likelihood function is derived from the transition density of the Ornstein–Uhlenbeck process:

Where θ = (a, b, σ) represents the parameter vector. The estimated parameters from our analysis:

• Speed of mean reversion (a): 0.7753
• Long-term mean (b): 0.0245
• Volatility (σ): 0.0056

CIR Model Calibration

The CIR model's non-Gaussian nature necessitates a different approach. We employ the Generalized Method of Moments (GMM), which matches theoretical and empirical moments of the rate series. This method is particularly well-suited for the CIR model due to its ability to handle the non-linear dynamics:

• First moment: E[rt] = b
• Second moment: Var(rt) = bσ²/2a
• Autocorrelation: ρ(τ) = e^{-aτ}

Our calibration results:

• Speed of mean reversion (a): 0.5710
• Long-term mean (b): 0.0190
• Volatility (σ): 0.0492

Monte Carlo Simulation Analysis

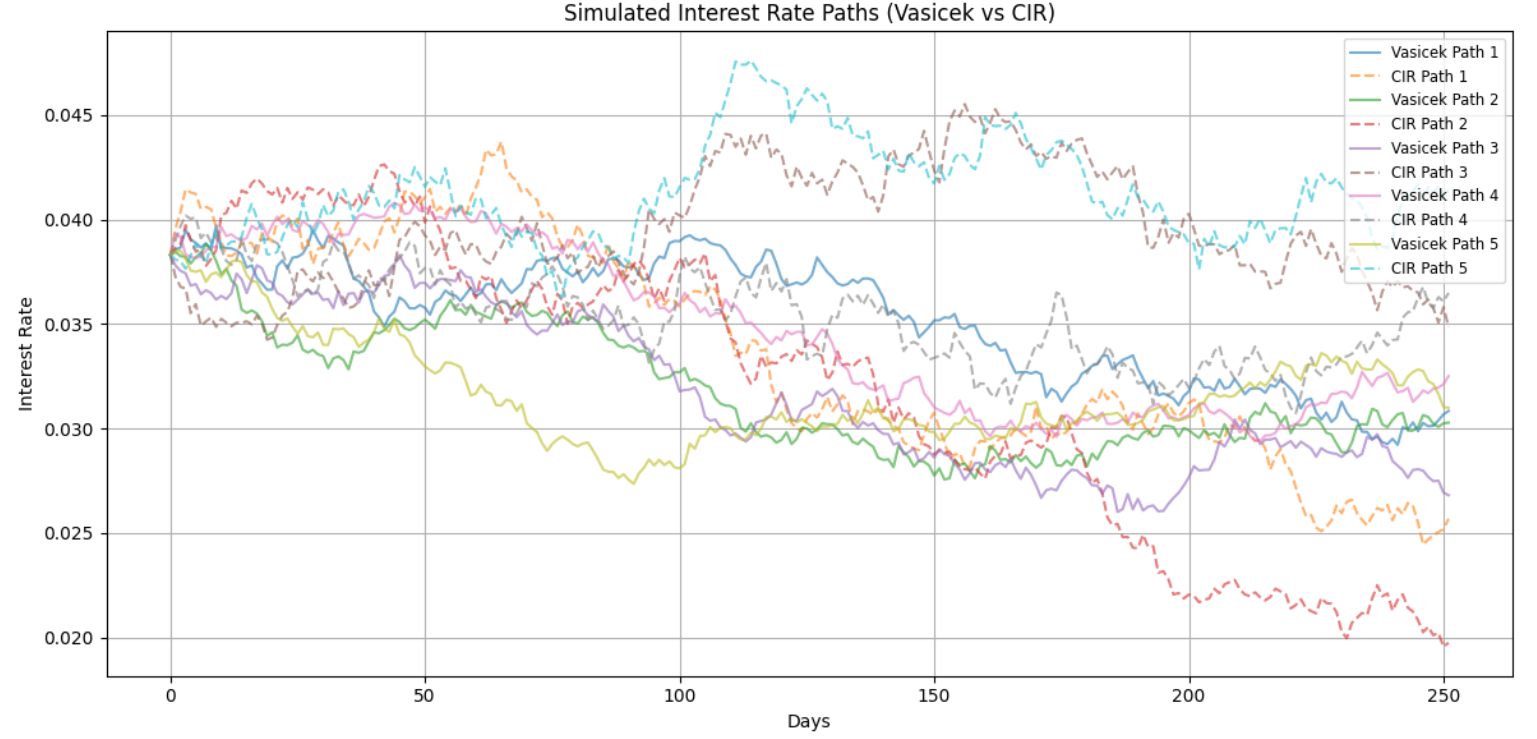
To validate our theoretical framework and parameter estimates, we conduct extensive Monte Carlo simulations using the Euler–Maruyama discretization scheme. This numerical approach allows us to explore the models' behavior under various scenarios:

Simulation Results

Our simulations of 1,000 paths over 252 trading days reveal important insights about the models' behavior. The initial conditions and parameters are calibrated against historical 1-year Treasury yield data from the U.S. Department of the Treasury, providing a realistic foundation for our forward projections:

Vasicek Model Characteristics

CIR Model Characteristics

These results highlight the fundamental differences between the models:

• The Vasicek model produces smoother paths due to constant volatility.
• The CIR model exhibits greater dispersion in extreme scenarios.
• Both models maintain strong mean-reverting properties.

Theoretical Implications and Applications

• Model Selection and Theoretical Considerations
  The choice between Vasicek and CIR models involves fundamental theoretical trade-offs. While the Vasicek model offers analytical tractability and closed-form solutions for bond prices, its allowance for negative rates may be theoretically problematic. The CIR model, while more complex, provides a more realistic representation of interest rate behavior by ensuring non-negativity through its square-root process.
• Risk Management Theory
  From a theoretical perspective, these models provide a robust framework for understanding interest rate risk. The mean-reverting property suggests that extreme rate movements are temporary, while the stochastic component captures the inherent uncertainty in financial markets. This theoretical foundation is crucial for developing effective risk management strategies.

Conclusion

The theoretical exploration of interest rate dynamics through the Vasicek and CIR models provides valuable insights into the nature of financial markets. These models, while developed decades ago, continue to offer a robust framework for understanding and modeling interest rate behavior. Their theoretical foundations remain relevant in today's complex financial landscape, serving as essential tools for both academic research and practical applications in quantitative finance.

As financial markets evolve, the theoretical principles underlying these models continue to guide our understanding of interest rate dynamics, risk management, and financial instrument valuation. The combination of theoretical rigor and practical applicability makes these models indispensable tools in the quantitative finance toolkit.

References